最高のコレクション x^2 y^2=1 circle 148893-X^2+y^2=1 unit circle
1
The distance formula will be used to find the distance from the center to one of the points on the circle This will yield the radius d = √(x2 − x1)2 (y2 − y1)2 d = √(7 − 3)2 (2 − ( − 1))2 d = 221 #2 Substitue y=mx4 into the circle equation x^2 (mx4)^2 = 2 (mx4) Find all m that gives exactly 1 solution for x You can use completing the square for x to
X^2+y^2=1 unit circle
X^2+y^2=1 unit circle-Consider the hyperbola H x 2 − y 2 = 1 and a circle S with center N (x 2, 0) Suppose that H and S touch each other at a point P (x 1, y 1) with x 1 > 1 and y 1 > 0 The common tangent to H and SExamples example 1 Find the center and the radius of the circle (x− 3)2 (y 2)2 = 16 example 2 Find the center and the radius of the circle x2 y2 2x− 3y− 43 = 0 example 3 Find the
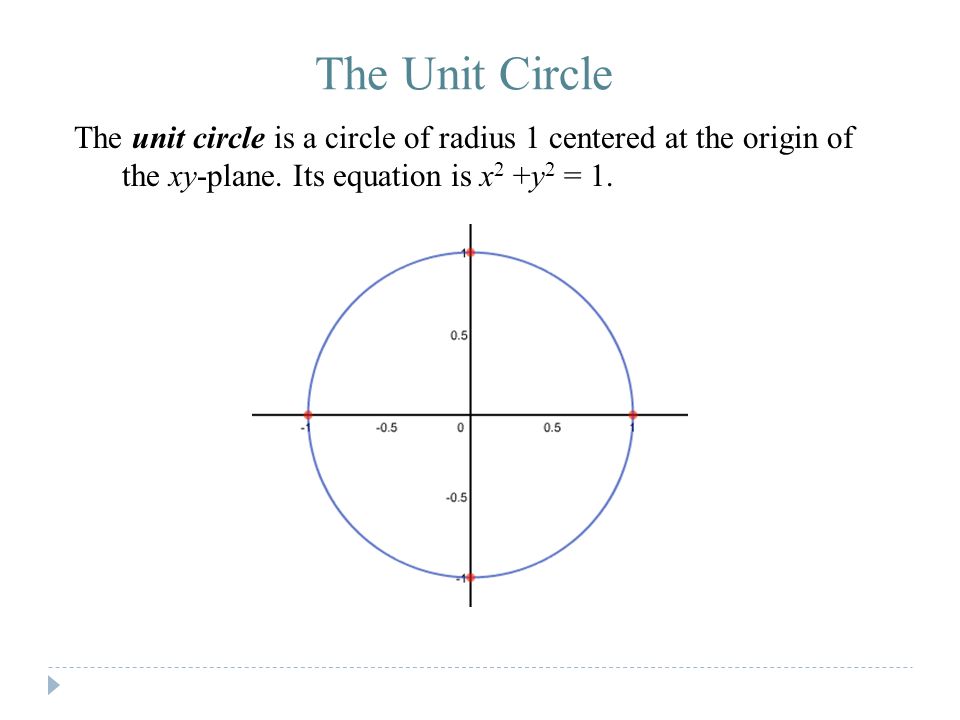
The Unit Circle The Unit Circle Is A Circle Of Radius 1 Centered At The Origin Of The Xy Plane Its Equation Is X 2 Y 2 Ppt Download
If we place the circle center at (0,0) and set the radius to 1 we get (x−a) 2 (y−b) 2 = r 2 (x−0) 2 (y−0) 2 = 1 2 x2 y2 = 1 Which is the equation of the Unit Circle If you write $x = cos(t)$ (it is possible since $0\leqslant x \leqslant 1$), then you can remark that $y^2 = 1x^2 = 1\cos ^2 (t)=\sin ^2 t$, so that you can write $y=\pm \sin t$ If $y=A circle is given by x^2 (y 1)^2 = 1 , another circle C touches it externally and also the x axis, then the locus of its centre is
Draw a circle of radius 3 cm From an external point 7 cm away from its centre, construct the pair of tangents to the circle and measure their lengths A pair of tangents are drawn from the origin toApplying Pythagoras theorem we have x 2 y 2 = 1 which represents the equation of a unit circle Also in a unit circle, we have, x = cosθ, and y = sinθ, and applying this in the above statement ofAlgebra Graph x^2y^2=1 x2 y2 = 1 x 2 y 2 = 1 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2
X^2+y^2=1 unit circleのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
「X^2+y^2=1 unit circle」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「X^2+y^2=1 unit circle」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「X^2+y^2=1 unit circle」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「X^2+y^2=1 unit circle」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「X^2+y^2=1 unit circle」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「X^2+y^2=1 unit circle」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「X^2+y^2=1 unit circle」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「X^2+y^2=1 unit circle」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「X^2+y^2=1 unit circle」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「X^2+y^2=1 unit circle」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「X^2+y^2=1 unit circle」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
Tap for more steps (x1)2 (y−2)2 = 4 ( x 1) 2 ( y 2) 2 = 4 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( yCircleareacalculator area x^2y^2=1 en
Incoming Term: x^2+y^2=1 circle, for the circle (x-1)^2+(y+1)^2=20, x^2+y^2=1 unit circle, consider three circles x^2+y^2=1, green's theorem circle x^2+y^2=1, consider a circle x^2+y^2=1, if the circle x^2+y^2=1 cuts the rectangular hyperbola, the circle with equation x^2+y^2=1 intersects the line, the circle with equation x^2+y^2=1, a circle c and x^2+y^2=1 are orthogonal,
コメント
コメントを投稿